3) Il livello due (Data Link)

Questo livello ha il compito di offrire una comunicazione affidabile ed efficiente a due macchine adiacenti, cioé connesse fisicamente da un canale di comunicazione (ad es.: cavo coassiale, doppino, linea telefonica).

Esso si comporta come un "tubo digitale", cioé i bit partono e arrivano nello stesso ordine. La cosa non è banale come sembra, perché:

• ci sono errori e disturbi occasionali;
• il canale ha un data rate finito;
• c'è un ritardo nella propagazione.

I protocolli usati per la comunicazione devono tenere in conto tutto questo.

Competenze del livello data link

Questo livello ha le seguenti incombenze principali:

• offrire servizi al livello network con un'interfaccia ben definita;
• determinare come i bit del livello fisico sono raggruppati in frame (framing);
• gestire gli errori di trasmissione;
• regolare il flusso della trasmissione fra sorgente e destinatario.

Servizi offerti al livello Network

Il servizio principale è trasferire dati dal livello network della macchina di origine al livello network della macchina di destinazione.

Come sappiamo, la trasmissione reale passa attraverso il livello fisico, ma noi ragioniamo in termini di dialogo fra due processi a livello data link che usano un protocollo di livello data link.

I servizi offerti possono essere diversi. I più comuni sono:

• connectionless non confermato
  • si mandano frame indipendenti;
  • i frame non vengono confermati;
  • non si stabilisce una connessione;
  • i frame persi non si recuperano (in questo livello);
  • è appropriato per:
    • canali con tasso d'errore molto basso;
    • traffico real-time (es. voce);
    • le LAN, nelle quali, in effetti, è molto comune.
• connectionless confermato
  • come sopra, però i frame vengono confermati;
  • se la conferma non arriva, il mittente può rispedire il frame;
  • è utile su canali non affidabili (ad es. in sistemi wireless);
  • nota 1: la perdita di un ack può causare la trasmissione di più copie dello stesso frame;
  • nota 2: avere la conferma a questo livello è un'ottimizzazione, mai una necessità. Infatti la conferma può sempre essere fatta a livello superiore, ma con linee disturbate ciò può essere gravoso.
• connection oriented confermato
  • è il servizio più sofisticato;
  • prevede tre fasi (apertura conn./invio dati/chiusura conn.);
  • garantisce che ogni frame sia ricevuto esattamente una volta e nell'ordine giusto;
  • fornisce al livello network un flusso di bit affidabile.

Vediamo ora un tipico esempio di funzionamento. Consideriamo un router con alcune linee in ingresso ed alcune in uscita. Ricordiamo che il routing avviene a livello tre (network), quindi il router gestisce i livelli uno, due e tre.

1. Quando al router arrivano dei bit da una linea fisica, l'hardware apposito se ne accorge (siamo a livello 1) e li passa al corrispondente SW/HW di livello due.
2. Il SW/HW di livello due (data link), che in genere è contenuto in un chip sulla scheda (o adattatore) di rete (tipico esempio è una scheda Ethernet) fa i controlli opportuni:
   • framing;
   • controllo errori di trasmissione;
   • controllo numero di frame (se necessario).
3. Se tutto è OK, il SW/HW di livello due genera un interrupt alla cpu, che chiama in causa il SW di livello tre (network):
   • questo è tipicamente un processo di sistema, al quale viene passato il pacchetto contenuto nel frame di livello due per l'ulteriore elaborazione;
   • l'elaborazione consiste nel determinare, sulla base delle caratteristiche del pacchetto (in particolare dell'indirizzo di destinazione), su quale linea in uscita instradarlo.
4. Presa questa decisione, il SW di livello tre consegna il pacchetto al corrispondente SW/HW di livello due, che lo imbusta in un nuovo frame e lo consegna al sottostante livello fisico (ossia quello relativo alla linea in uscita prescelta).

Il livello uno accetta un flusso di bit grezzi e cerca di farli arrivare a destinazione. Però:

• il flusso non è esente da errori;
• possono arrivare più o meno bit di quanti sono stati inviati.

E' compito del livello due rilevare, e se possibile correggere, tali errori. L'approccio usuale del livello due è il seguente.

• In trasmissione:
  • spezza il flusso di bit che arriva dal livello tre in una serie di frame;
  • calcola un'apposita funzione (checksum) per ciascun frame;
  • inserisce il checksum nel frame;
  • consegna il frame al livello uno, il quale lo spedisce come sequenza di bit.
• In ricezione:
  • riceve una sequenza di bit dal livello uno;
  • ricostruisce da essa un frame dopo l'altro;
  • per ciascun frame ricalcola il checksum;
  • se esso è uguale a quello contenuto nel frame questo viene accettato, altrimenti viene considerato errato e quindi scartato.

Dunque, la prima cosa (più difficile di quanto sembri) di cui occuparsi, è come delimitare un singolo frame.

3.1) Framing

E' rischioso usare lo spazio temporale che intercorre tra i frame per delimitarli, perché nelle reti in genere non ci sono garanzie di temporizzazione. Quindi, si devono usare degli appositi marcatori per designare l'inizio e la fine dei frame.

Ci sono vari metodi:

• conteggio dei caratteri;
• caratteri di inizio e fine, con character stuffing;
• bit pattern di inizio e fine, con bit stuffing;
• violazioni della codifica dei bit usata nel livello fisico.

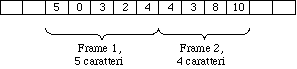
3.1.1) Conteggio

Si utilizza un campo nell'header, per indicare quanti caratteri ci sono del frame

Se durante la trasmissione si rovina il campo del frame che contiene il conteggio, diventa praticamente impossibile ritrovare l'inizio del prossimo frame e di conseguenza anche quello dei successivi. A causa della sua scarsa affidabilità questo metodo è usato ormai pochissimo.

3.1.2) Caratteri di inizio e fine

Ogni frame inizia e finisce con una particolare la sequenza di caratteri ASCII.

Una scelta diffusa è la seguente:

• inizio frame:
  • DLE (Data Link Escape), STX (Start of TeXt)
• fine frame:
  • DLE, ETX (End of TeXt)

In questo modo, se la destinazione perde traccia dei confini di un frame la riacquista all'arrivo della prossima coppia DLE, STX e DLE, ETX.

Esiste però un problema: nella trasmissione di dati binari, il byte corrispondente alla codifica di DLE può apparire dentro il frame, imbrogliando le cose.

Per evitare questa evenienza, il livello due sorgente aggiunge davanti a tale byte un altro DLE, per cui in arrivo solo i singoli DLE segnano i confini dei frame. Naturalmente, il livello due di destinazione rimuove i DLE aggiunti dentro ai dati prima di consegnarli al livello tre. Questa tecnica si chiama character stuffing.

3.1.3) Bit pattern di inizio e fine

La tecnica precedente è legata alla codifica ASCII ad 8 bit, e non va bene per codifiche più moderne (es. UNICODE). Una tecnica analoga e più recente permette di avere un numero qualunque di bit dentro il frame.

Ogni frame inizia e finisce con una specifica sequenza di bit (bit pattern), ad es.:

chiamata un flag byte.

Ovviamente esiste un problema analogo al caso precedente: tale sequenza di bit può infatti apparire all'interno dei dati che devono essere trasmessi.

In questo caso:

• in trasmissione: ogni volta che il livello due incontra nei dati da trasmettere 5 bit consecutivi uguali a 1 inserisce uno zero aggiuntivo;
• in ricezione: quando nei dati ricevuti compaiono 5 bit uguali a uno, si rimuove lo zero che li segue.

Dunque, il flag byte può apparire solo all'inizio ed alla fine dei frame. Questa tecnica va sotto il nome di bit stuffing.

3.1.4) Violazioni della codifica

In molte reti (sopratutto LAN) si codificano i bit al livello fisico con una certa ridondanza. Ad esempio:

• il valore 1 di un bit di dati è codificato con la coppia high/low di bit fisici;
• il valore 0 di un bit di dati è codificato con la coppia low/high di bit fisici.

Le coppie low/low ed high/high non sono utilizzate. Codifiche come questa (Manchester encoding, usata in IEEE 802.3) hanno lo scopo di consentire una facile determinazione dei confini di un bit dati, poiché esso ha sempre una trasmissione nel mezzo (però ci vuole una bandwidth doppia per trasmetterlo a parità di velocità).

Le coppie high/high e low/low possono quindi essere usate per delimitare i frame.

3.2) Rilevamento e correzione errori

Ci sono molti fattori che possono provocare errori, sopratutto sul local loop e nelle trasmissioni wireless. Viceversa, essi sono piuttosto rari nei mezzi più moderni quali le fibre ottiche.

Gli errori sono dovuti in generale a:

• rumore di fondo;
• disturbi (ad es. fulmini) improvvisi;
• interferenze (ad es. motori elettrici).

Ci sono due approcci al trattamento degli errori:

• includere abbastanza informazione aggiuntiva in modo da poter ricostruire il messaggio originario (correzione dell'errore);
• includere meno informazione aggiuntiva, in modo da accorgersi che c'è stato un errore, senza per questo essere in grado di correggerlo (rilevazione dell'errore).

3.2.1) Codici per la correzione degli errori

Normalmente, un frame (a parte i delimitatori) consiste di

bit, dove:

• m bit costituiscono il messaggio vero e proprio;
• r bit sono ridondanti, e sono detti reduntant bit (o check bit).

Una sequenza di n bit fatta in tal modo si dice codeword, o parola di codice.

Date due qualunque parole di codice, ad es.:

è possibile determinare il numero di bit che in esse differiscono (tre nell'esempio) tramite un semplice XOR fatto bit a bit.

Tale numero si dice la distanza di Hamming delle due codeword (Hamming, 1956). Se due codeword hanno una distanza di Hamming uguale a d, ci vogliono esattamente d errori su singoli bit per trasformare l'una nell'altra.

Un insieme prefissato di codeword costituisce un codice (code). La distanza di Hamming di un codice è il minimo delle distanze di Hamming fra tutte le possibili coppie di codeword del codice.

Ora, le capacità di rilevare o correggere gli errori dipendono strettamente dalla distanza di Hamming del codice scelto.

In particolare:

• per rilevare d errori serve un codice con distanza di Hamming (d+1). Infatti, in questo caso qualunque combinazione di d errori non riesce a trasformare un codeword valido in un altro codeword valido, per cui si ha per forza un codeword non valido, che quindi rivela il fatto che ci sono stati degli errori;
• per correggere d errori, serve un codice di Hamming con distanza (2d+1). Infatti in questo caso un codeword contenente fino a d errori è più vicino a quello originario che a qualunque altro codeword valido.

Dunque, a seconda degli scopi che si vogliono raggiungere, si progetta un algoritmo per il calcolo degli r check bit (in funzione degli m bit del messaggio) in modo che i codeword di n = m + r bit risultanti costituiscano un codice con la desiderata distanza di Hamming.

Vediamo ora, come esempio, un codice ottenuto mediante l'aggiunta di un bit di parità, calcolato in modo tale che il numero totale di bit uguali ad 1 sia pari (in questo caso si parla di even parity)

Questo codice, detto codice di parità (parity code) ha distanza di Hamming uguale a due, e dunque è in grado di rilevare singoli errori. Infatti, un singolo errore produce un numero dispari di 1 e quindi un codeword non valido.

Come secondo esempio, consideriamo il codice costituito dalle seguenti codeword:

Esso ha distanza 5, per cui corregge due errori (cifre sottolineate). Infatti, se arriva

si può risalire correttamente al codeword più vicino, che è

Però, se ci sono tre errori ed arriva

siamo nei guai, perché esso verrà intrepretato erroneamente come

anziché come

Per correggere un singolo errore su m bit, si devono impiegare almeno r check bit, con

ossia sono necessari circa lg₂ m bit. Esiste un codice (codice di Hamming) che raggiunge questo limite teorico.

Ora, c'è una semplice tecnica con la quale tale codice può essere impiegato per correggere gruppi contigui di errori (detti burst di errori) di lunghezza massima prefissata.

Supponiamo di voler correggere burst di lunghezza k:

• si accumulano k codeword, riga per riga;
• i codeword si trasmettono per colonne;
• quando arrivano si riassemblano per righe. Un burst di k errori comporta un singolo errore in ciascun codeword, che quindi può essere completamente ricostruito.

3.2.2) Codici per il rilevamento degli errori

I codici correttori di errore sono usati raramente (ad esempio in presenza di trasmissioni simplex, nelle quali non è possibile inviare al mittente una richiesta di ritrasmissione), perché in generale è più efficiente limitarsi a rilevare gli errori e ritrasmettere saltuariamente i dati piuttosto che impiegare un codice (più dispendioso in termini di ridondanza) per la correzione degli errori.

Infatti, ad esempio, supponiamo di avere:

• canale con errori isolati e probabilità di errore uguale a 10^-6 per bit;
• blocchi dati di 1.000 bit.

Per correggere errori singoli su un blocco di 1.000 bit, ci vogliono 10 bit, per cui un Megabit richiede 10.000 check bit.

Viceversa, per rilevare l'errore in un blocco, basta un bit (con parity code). Ora, con 10^-6 di tasso d'errore, solo un blocco su 1.000 è sbagliato e quindi deve essere ritrasmesso. Di conseguenza, per ogni Megabit si devono rispedire 1.001 bit (un blocco più il parity bit).

Dunque, l'overhead totale su un Megabit è:

• 1.000 bit per parity bit su 1.000 blocchi,
• 1.001 bit per il blocco ritrasmesso,
• per un totale di 2.000 bit contro i 10.000 del caso precedente.
  

L'uso del parity bit può servire (con un meccanismo analogo a quello visto per la correzione di burst di k errori) per rilevare burst di errori di lunghezza <= k. La differenza è che non si usano r check bit per ogni codeword, ma uno solo.

Esiste però un altro metodo che nella pratica viene usato quasi sempre, il Cyclic Redundancy Code (CRC), noto anche come polynomial code. I polynomial code sono basati sull'idea di considerare le stringhe di bit come rappresentazioni di polinomi a coefficenti 0 e 1 (un numero ad m bit corrisponde ad un polinomio di grado m-1).

Ad sempio, la stringa di bit 1101 corrisponde al polinomio x³ + x² + x⁰.

L'aritmetica polinomiale è fatta modulo 2, secondo le regole della teoria algebrica dei campi. In particolare:

• addizione e sottrazione sono equivalenti all'or esclusivo (non c'è riporto o prestito);
• la divisione è come in binario, calcolata attraverso la sottrazione modulo 2.

Il mittente ed il destinatario si mettono d'accordo su un polinomio generatore G(x), che deve avere il bit più significativo e quello meno significativo entrambi uguali ad 1. Supponiamo che G(x) abbia r bit.

Il frame M(x), del quale si vuole calcolare il checksum, dev'essere più lungo di G(x). Supponiamo che abbia m bit, con m > r.

L'idea è di appendere in coda al frame un checksum tale che il polinomio corrispondente (che ha grado m + r -1) sia divisibile per G(x).

Quando il ricevitore riceve il frame più il checksum, divide il tutto per G(x). Se il risultato è zero è tutto OK, altrimenti c'è stato un errore.

Il calcolo del checksum si effettua come segue:

1. Appendere r bit a destra del frame, che quindi ha m+r bit, e corrisponde ad x^rM(x);
2. Dividere x^rM(x) per G(x);
3. Sottrarre ad x^rM(x) il resto della divisione effettuata al passo precedente. Ciò che si ottiene è il frame più il checksum da trasmettere, che è ovviamente divisibile per G(x). Si noti che di fatto questa è un'operazione di XOR fatta sugli r bit meno significativi, e quindi non modifica il frame.

Questo metodo è molto potente, infatti un codice polinomiale con r bit:

• rileva tutti gli errori singoli e doppi;
• rileva tutti gli errori di x bit, x dispari;
• rileva tutti i burst di errori di lunghezza <= r.

Tra i polinomi sono diventati standard internazionali:

• CRC-12: x¹² + x¹¹ + x³ + x² + x¹ + 1;
• CRC-16: x¹⁶ + x¹⁵ +x² + 1;
• CRC-CCITT: x¹⁶ + x¹² + x⁵ + 1;

Un checksum a 16 bit corregge:

• errori singoli e doppi;
• errori di numero dispari di bit;
• errori burst di lunghezza <= 16;
• 99.997% di burst lunghi 17;
• 99.998% di burst lunghi 18.

Questi risultati valgono sotto l'ipotesi che gli m bit del messagio siano distribuiti casualmente, il che però non è vero nella realtà, per cui i burst di 17 e 18 possono sfuggire più spesso di quanto si creda.